A few days ago in gr-qc  journal club we discussed an interesting paper by a member of our own institute, Probing the dark matter issue in f(R)-gravity via gravitational lensing.¹.

Background

Figure from: http://en.wikipedia.org/wiki/Dark_matter. This is the rotation curve, or velocity vs. radius of a typical spiral galaxy. A is predicted, B is observed. We can bring A and B into agreement in our best theory of gravity by invoking dark matter.

Dark Matter

We theoretically expect dark matter to exist based largely on  extensive observations of both dynamics (rotation curves and objects such as the Bullet Cluster) and gravitational lensing data. Rotation curves show that in our current best gravitational theory, general relativity, there must be a lot of unaccounted for mass to explain the speed of the rotation of objects on the outskirts of galaxies. Furthermore, gravitational lensing data shows large amounts of unseen mass bending light.

Experimental particle physicists and theorists are hard at work searching for the dark matter particle and there are many potential physical models which incorporate a particle of a mass consistent with current observations. The constraints on what the particle could be get more and more precise and the hope is to discover or constrain out of existence the particle physics explanation for the rotation curves and gravitational lensing observations. If the former occurs astrophysical theorists will be extremely happy as we regularly blithely invoke dark matter in our models waiting for the experiments to catch up. If the latter occurs, many are working hard at considering alternatives the most plausible seeming to be some modification of General Relativity.

Alternatives

GR is in some sense the theory having the simplest equations encapsulating the connection between mass-energy and the curvature of space. Any modification makes the equations more complicated and as result less appealing. Moreover we have many precision measurements, especially in the solar system, confirming GR. Due to these measurements, any modification usually contains contortions to make it match observations and are as a consequence more kludgy, hokey and moreover not fully successful, in the mind of most theorists, to date as matching the range of observations we have. A modified gravity theory will often attempt to  modify the GR equations by generalizing them in some manner, derive the consequences of this modification (often the theory was designed with particular consequences in mind such as no longer requiring dark matter to match predictions), then seeing what “broke” (which predictions no longer match observation) and fixing it with some mathematical duct tape, wherever possible.

f(R) gravity

Modified 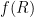gravity is one of the simplest modifications of GR we can consider. R is the scalar curvature, also known as the Ricci scalar-which is itself determined from the metric, the mathematical object incorporating all the information we need to know in math-land about the geometry of space. In modified 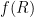gravity the standard starting equation to derive the Einstein-Field equations (in physics terms the Einstein-Hilbert action), containing R, is modified to rather contain a function of R, 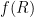, hence its name. Thus, when we derive the field equations, they are themselves modified.

,

Shows lensing (enlarge and look for the arcs) and fitting for the mass of the lens to produce the arcs indicates the presence of a large amount of unseen matter. Figure from: NASA, N. Benitez (JHU), T. Broadhurst (Racah Institute of Physics/The Hebrew University), H. Ford (JHU), M. Clampin (STScI),G. Hartig (STScI), G. Illingworth (UCO/Lick Observatory), the ACS Science Team and ESA derivative work

Results

The interesting result of this paper is essentially that in  gravity, the theoretical expectations of lensing observations remain unchanged from standard general relativity. That is to say, since standard GR needs to invoke dark matter to explain the lensing data, so does gravity.

The consequence of this is important,  One large reason to invoke modified gravity, even in the face of its necessary contortions and duct tape, is that it could have the potential to provide an explanation alternative to dark matter for the rotation curves and the gravitational lensing information. This paper shows that for gravity it could potentially explain only one of the two removing some of the appeal of going through the theoretical pain of modifying a well tested and understood theory.

References

1. M. Lubini, C. Tortora, J. Näf, Ph. Jetzer, & S. Capozziello (2011). Probing the dark matter issue in f(R)-gravity via gravitational lensing arXiv: 1104.2851v1